Jessica's solution to a loopy problem

A well known algorithm, taught in Number Theory classes at tertiary level, is Euclid’s algorithm for finding the Greatest Common Divisor (GCD) of two numbers. In Australia, we tend to refer to the GCD as the Highest Common Factor. In this post, I describe the algorithm and present a year 8 student’s program that implements it.

The Algorithm

To illustrate what the GCD of two numbers is, let’s consider a 21 x 15 rectangle.

Saying that the GCD of 21 and 15 is 3 is the same as saying that 3x3 is the largest square that can be used to partition the area of a 21x15 rectangle without any “left-overs”.

But what if we were asked the GCD of 1989 and 867, the example used in wikipedia’s description of the algorithm? I, for one, don’t have the patience to draw up this example. Thankfully, Euclid has worked out a systematic way to find this.

Euclid’s algorithm (one version of it anyway) says that, given two numbers a and b, we should keep on replacing the larger of the two numbers with the difference (a - b or b - a) until both numbers are the same. At that point, we will have found the GCD. For example, let’s find the GCD of 72 and 30:

Here we have it, the GCD of 72 and 30 is 6.

How the APP Group  went with it

Yesterday, at APP group (after school club), we warmed up with a few simple Scratch programs involving loops (repeat blocks). We basically generated the even numbers between 2 and 20. I then challenged the students (32 girls between years 8 and 11) to find all the even numbers between 60 and 98

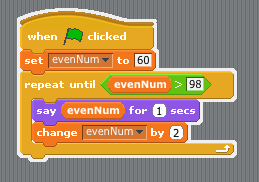Scratch script for displaying even numbers between 60 and 98

The Scratch cat "saying" the even numbers

I then described Euclid’s algorithm to them with a simple example: finding the GCD of 12 and 8. As I was about to give them a slightly harder example, my colleague Steven challenged them to find the GCD of 72 and 30 (see example above). They did it with pen and paper, some of them struggling a bit and others solving it quite quickly. As with the even numbers challenge, a few year 8s were the first to find the solution. The year 8s really shone yesterday with their solutions and demonstrations to their peers.

Straight after that, I said: “who thinks she can write a Scratch program that implements this algorithm?” Steven looked at me as though to say: “they will need more clues”. After all, they hadn’t seen a formal version of the algorithm. So I told them, “You need to ask the user for two numbers and use a ‘repeat until loop’”. Steven and I gave more hints to individual students as we saw necessary.

Much to my amazement and Steven’s, a year 8 girl called Jessica Clear-Thinker solved it in a little over 10 minutes. Her solution appears at the end of this post. I hope it is readable regardless of whether you have had prior experience with Scratch or not. The solution does not take special cases into account, notably when one of the numbers is zero. Still, it is a great first time application of loops to a real mathematical problem.

I want to acknowledge Steven (the incredible Mr Francis) as the inspiration for this meeting’s theme. He had planted the idea in my mind using a three-pronged approach: subliminal, liminal and superliminal (a joke for the Simpsons’ fans out there)! 

Back to Jessica Clear-Thinker: You’ll be happy to know that I broke my rule on extraneous rewards and raced to my desk to get her a chocolate.

Jessica's implementation of Euclid's algorithm for finding GCD