Dots, numbers and the mind of a child-genius

This post will show some beautiful and simple arithmetic. We will represent a seemingly complex question using triangles and and see how, at 8 years of age, famous 19th century mathematician Gauss added all the whole numbers from 1 to 100 in seconds. 

How many dots in the triangle?

Here are a few triangles, drawn with dots only:

                    A triangle with 2 levels and 3 dots

 

             A triangle with 3 levels and 6 dots

    A triangle with 4 levels and 10 dots

Notice that each triangle answers the question, what is the sum of the whole numbers from 1 to the last level of the triangle? 

• The triangle with 2 levels has 1 + 2 = 3 dots
• The triangle with 3 levels has 1 + 2 + 3 = 6 dots
• The triangle with 4 levels has 1 + 2 + 3 + 4 = 10 dots

The story of Gauss

Carl Friedrich Gauss was a German mathematician from the first half of the 19th century. When he was eight, his teacher could not keep him occupied in class: He solved maths problems too quickly! The teacher thought it would surely take Gauss quite some time to add up the whole numbers from 1 to 100. Well, it took him no time at all to work out that the answer was 5050.

Gauss could have drawn a triangle of dots, starting with one dot at the top and ending with 100 dots at the bottom. That would have taken quite some time and delighted his teacher! Instead, he had the insight to line up the numbers like so:

Gauss realised that the numbers to be added form 50 pairs. Each pair adds up to 101. In total, we have 50 groups of 101 or:

Let's be mini-Gausses!

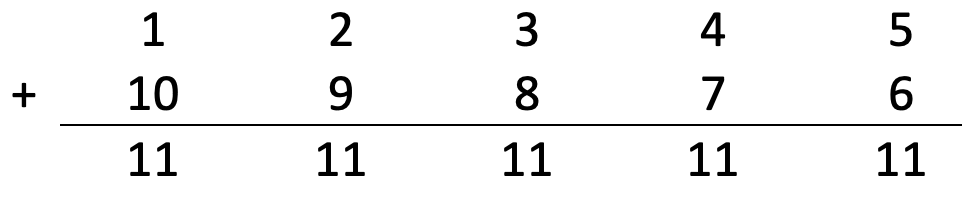
Let's do the same as Gauss, but for a smaller maximum number. Let's calculate 1 + 2 + 3 + ... + 10.

That's 5 pairs, each adding up to 11, or:

What if we wanted the sum from 1 to 20? Well, we would have 10 pairs of numbers, each adding up to 21.

The sum up to 30? 15 pairs, adding up to 31.

etc.

The general case and a hanging question

In general, to find the sum of the whole number between 1 and some maximum number, n, we will have 

I know what you're wondering: What if Gauss had been asked to add the whole numbers from 1 to 99? Surely, 99 numbers cannot be paired up? Well, there is a way to do it. If you're interested, let me know in the comments and I'll write a post about that.